3 ferramentas importantes de pesquisa de operação
Este artigo lança luz sobre as três importantes ferramentas de pesquisa operacional. As ferramentas são: 1. Programação Linear 2. Problemas de Transporte 3. Problema de Atribuição.
Pesquisa de Operação: Ferramenta nº 1. Programação Linear:
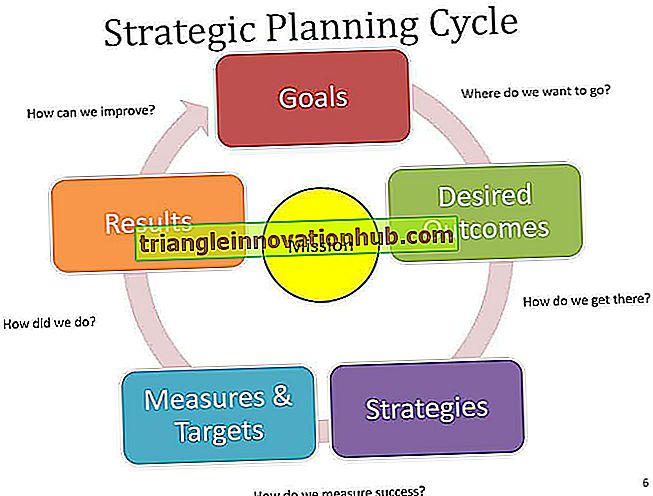
A programação linear é uma técnica matemática que tem aplicação em quase todas as classes de problemas de decisão. Esta técnica é aplicada para escolher como a melhor alternativa de um conjunto de alternativas possíveis.
Na função de objetivo LPP, bem como as restrições podem ser expressas como função matemática linear, que pode ser usada para resolver os problemas práticos de programação. É um método usado para estudar o comportamento dos sistemas.
LP está principalmente preocupado em descrever a inter-relação dos componentes de um sistema. Essa técnica é projetada para ajudar os gerentes no planejamento, na tomada de decisões e na alocação de recursos. A gerência sempre tem a tendência de fazer o uso mais eficaz de um recurso da organização. Os recursos incluem matérias-primas de máquinas, mão de obra, depósito, tempo e dinheiro.
Esses recursos podem ser utilizados para produzir produtos de vários tipos, que podem ser máquinas, peças / componentes, móveis e produtos alimentícios, etc. Da mesma forma, recursos podem ser usados para fornecer serviços, como cronograma de remessa, políticas de propaganda e decisões de investimento.
Todas as organizações precisam tomar decisões sobre a alocação de seus recursos limitados. Portanto, os gerentes são obrigados a alocar continuamente recursos escassos para atingir as metas / objetivos / metas da organização.
O adjetivo linear foi usado para descrever uma relação entre duas ou mais variáveis. A programação diz respeito ao uso de certas equações matemáticas usadas para obter a melhor solução possível para um problema envolvendo recursos limitados / escassos.
Assim, a programação linear é usada para problemas de otimização que satisfaçam a seguinte condição:
(i) A função objetivo a ser otimizada deve ser bem definida e expressa como uma função linear das variáveis.
(ii) A limitação, se houver, da realização desses objetivos também é expressa como qualidades lineares / desigualdades de variável.
(iii) Alguns cursos alternativos de ações também estão disponíveis.
(iv) As variáveis de decisão estão inter-relacionadas e não são negativas.
(v) Recursos são limitados.
Aplicação de Programação Linear a Problemas Industriais:
(i) Desenvolver agendamento para indústrias de processamento de alimentos e para refinarias de petróleo, etc.
(ii) Nas indústrias metalúrgicas, é utilizado para o carregamento de lojas e para determinar a escolha entre comprar e produzir várias peças.
(iii) É usado para avaliar vários minérios de ferro nas indústrias de ferro e aço.
(iv) É usado para reduzir a quantidade de perdas de guarnição nas fábricas de papel.
(v) É utilizado para encontrar o melhor roteamento de mensagens na rede de comunicação.
Definição de programação linear:
A programação linear é uma ferramenta / técnica matemática para determinar os melhores usos dos recursos de uma organização. A programação linear é projetada para ajudar os gerentes no planejamento e na tomada de decisões. Como ferramenta de tomada de decisão, mostrou seu valor em diferentes áreas, como a produção; financiamento de marketing, pesquisa e contratação de pessoal.
Determinação do mix de produtos ideal, atribuição de máquinas de seleção de portfólio de cronogramas de transporte; localização da planta e alocação do trabalho etc. são os poucos tipos de problemas que podem ser resolvidos com a ajuda da programação linear.
“A análise de problemas nos quais uma função linear de um número de variáveis deve ser maximizada (ou minimizada) quando essas variáveis estão sujeitas ao número de restrições na forma de lineares em igualdades.”, Samuelson e Slow
De acordo com Loomba, “A programação linear é apenas um aspecto do que tem sido chamado de abordagem sistêmica para o gerenciamento, em que todos os programas são projetados e avaliados em termos de seus efeitos finais na realização dos objetivos de negócios”.
Método Gráfico-Problemas de Programação Linear:
As etapas do método gráfico podem ser resumidas da seguinte forma:
1. Formule o problema de programação linear.
2. Plote as linhas de restrição dadas considerando-as como equações.
3. A partir do gráfico acima, identifique a região viável da solução.
4. Localize os pontos de canto da região de solução viável.
5. Calcule o valor da função objetivo nos pontos do canto.
6. Agora, escolha o ponto em que a função objetivo tem valor ótimo.
Solução Matemática-Problemas de Programação Linear:
Embora o método gráfico de resolver LPP seja uma ajuda valiosa para entender sua estrutura básica. O método é de utilidade limitada em problemas industriais, uma vez que o número de variáveis que ocorrem lá é substancialmente grande. Assim, uma outra solução matemática chamada de método simplex é adequada para resolver LPP com um grande número de variáveis.
É um procedimento iterativo que resolve o LPP em um número finito de passos ou fornece uma indicação de que existe uma solução ilimitada para o método L.PR Simplex é um procedimento algébrico para resolver problemas de programação linear ou é composto de uma série de etapas repetitivas para alcançar uma solução ideal.
É um algoritmo de programação mais amplamente utilizado e mais geralmente usado. Teoricamente, este procedimento pode resolver qualquer problema que consista em qualquer número de variáveis e restrições. Se o problema consistir em mais de três variáveis e três restrições, o uso do computador é necessário. A Fig. 31.9 mostra a representação esquemática do algoritmo simplex.

Várias etapas no procedimento simplex:
As etapas deste procedimento estão listadas abaixo:
1. Formule o problema determinando a função objetiva e as restrições.
2. Converta as desigualdades em igualdades para obter a forma padrão, introduzindo excedente de folga e variáveis artificiais na função objetivo.
3. Prepare a tabela simplex inicial.
4. Calcule o valor de zj (perda líquida por unidade) e c j - z j (contribuição líquida) para esta solução.
5. Determine a variável de entrada (coluna-chave) selecionando a coluna com maior número negativo
(z j - c j ).
6. Determine a variável que parte (linha chave) calculando a coluna de razão da regra 5 e escolhendo o menor valor não negativo.
7. Calcule a linha de substituição da tabela simplex aprimorada pela regra 6.
8. Calcule as linhas restantes da nova tabela pela regra 7.
9. Calcule o valor de cj e zj para esta solução.
10. Se houver valor não negativo (c j - z j ), retorne ao passo 5.
11. Se não houver valores não negativos (c j - z j ), a solução ótima foi obtida.
Exemplo 1:
Um agricultor tem 1000 acres de terra em que ele pode plantar milho, trigo ou soja. Cada acre de milho custa Rs. 100 para preparação, requer 7 dias homem de trabalho e produz um lucro de Rs. 30 Um acre de trigo custa Rs. 120 para preparar, exigem 10 dias de trabalho do homem e geram um lucro de Rs. 40.
Um acre de soja custa Rs70 para se preparar requer 8 dias de trabalho e produz um lucro de Rs. 20 Se o agricultor tiver Rs. 100.000 para preparação e contar com 8000 dias de trabalho. Quantos acres devem ser alocados a cada cultura para maximizar os lucros? (MBA de Gujarat, 1989)
Solução:
Deixe x acre de terra ser alocado para o milho
y acres de terra serão alocados para trigo
z acre de terra ser alocado para soja
Uma vez que cada acre de terra para o milho produz um lucro de Rs. 30, para rendimentos de trigo Rs. 40 e para soja Rs. 20. A formulação matemática do LLP é
Máx. Z = 30x + 40y + 20z + 0S 1, + OS 2, + 0S 3
Sujeito a
100 x + 120y + 70z ≤ 100000
7x + 10a + 8z ≤ 8000
x + y + z ≤ 1000
x, y, z ≥ 0
Vamos converter as desigualdades em equações introduzindo as variáveis de folga S 1, S 2 e S 3 . A função objetivo e a restrição podem ser escritas como

Na coluna variável básica os vetores são para a variável S 1, (1, 0, 0), S 2, (1, 0, 1) e S 3 (0, 0, 1) a solução factível inicial é dada pelas variáveis S 1, S 2 e S 3, lucro total = 0
Agora Zj e Cj - Zj, são calculados pela Regra 1, 2 e 3. A coluna chave é determinada com a coluna marcada como início e a Tabela Simplex II é preparada como segue.

A tabela II não fornece a solução ótima que prosseguimos para preparar a tabela simples III e melhorar a solução como se segue:

Problema de Minimização pelo Método Big M.
Na indústria pode-se situar onde o objetivo pode ser minimizar o custo de produção ou a duração da fabricação, isto é, a função objetiva deve ser minimizada em tais casos, podemos proceder da mesma maneira como um problema de maximização simplesmente multiplicando por ambos os lados da função objetivo by-1 Em tais situações, a minimização de Z será a maximização de (-Z).
Em tais casos, uma vez que as variáveis excedentes tomam um valor negativo que viola a restrição de não negatividade, para superar essa dificuldade, introduzimos novas variáveis denominadas variáveis artificiais.
Agora, atribuímos o coeficiente 3000 às variáveis excedentes e + M às variáveis artificiais. Para fazer a fonte que as variáveis artificiais não são as variáveis básicas na solução ótima, atribuímos a elas um custo muito alto, portanto, M é definido como um número muito grande. ou penalidade.
Este método é ilustrado com a ajuda do seguinte:
Exemplo 2:


Pesquisa de Operação: Ferramenta nº 2. Problemas de Transporte:
Os problemas de transporte são um dos tipos de LPP cujo objetivo é transportar mercadorias / produtos em várias quantidades de um único item homogêneo / mercadoria para diferentes destinos, a fim de minimizar o custo total de transporte na vida cotidiana das várias organizações de manufatura ou outros estabelecimentos. a várias considerações armazenam seus produtos finais ou itens em vários lugares denominados origens ou ware, house quando o fornecimento é feito aos usuários e os itens são transportados das origens para um ou mais destinos, o objetivo geral desse processo é decidir uma política de distribuição tal que o custo total de transporte é mínimo ou o tempo consumido no transbordo é mínimo.
Depois que os produtos terminados nativamente da fábrica forem transportados para os armazéns da maneira mais econômica nos problemas de transporte, várias características da programação linear podem ser observadas. A disponibilidade e os requisitos de vários centros são finitos e constituem os problemas de transporte de recursos limitados. do método simplex.
Aplicação em válvulas o transporte de produtos de várias fontes para vários pontos de destino, tais como:
(i) unidades de transporte de destino rasgado. O objetivo é minimizar o custo de transporte.
(ii) Maximizar o lucro no transporte das unidades para o destino.
Os principais passos envolvidos são :
Passo 1:
Formule o problema e monte na forma de matriz de transporte.
Passo 2:
Obtenha a solução básica viável.
Etapa 3:
Teste para otimalidade da solução.
Passo 4:
Atualize a solução por meio de melhorias de sucesso até que não seja possível reduzir ainda mais o custo do transporte.
Métodos comumente usados são:
1. Método do canto noroeste.
2. Método de menor custo.
3. Método de Aproximação de Vogel.
Passos Envolvidos no Método do Canto do Noroeste:
Passo 1:
Construa uma matriz máxima vazia concluída com linhas e colunas.
Passo 2:
Indique os totais da linha e os totais da coluna no final.
Etapa 3:
Começando com (11) célula no canto noroeste da matriz, aloque a quantidade / número máximo possível, tomando cuidado para que a alocação não possa ser maior do que a quantidade requerida pelos respectivos armazéns nem mais do que a quantidade disponível nos centros de abastecimento.
Passo 4:
Depois de fazer o ajuste dos números de oferta e demanda nas respectivas alocações de linhas e colunas, mova para baixo até a primeira célula de e linha repita a etapa 3.
Passo 5:
Depois que a demanda da primeira coluna for satisfeita, faça a próxima célula na segunda coluna e na primeira linha e vá para a etapa 3.
Passo 6:
Se para qualquer suprimento de célula for igual a demanda, a próxima alocação pode ser o modo em células nas próximas linhas e colunas.
Passo 7:
Continue o processo até que a quantidade total disponível seja totalmente alocada para as células conforme a necessidade

Exemplo 3:
Resolva o seguinte problema pelo NWCM para calcular o custo mínimo de transporte:

Etapas no método de entrada de menor custo:
Este método leva em consideração o menor custo e, portanto, leva menos tempo para resolver o problema. As várias etapas são as seguintes:
Passo 1:
Selecione a célula com menor custo de transporte entre todas as linhas e colunas da matriz. Aloque o máximo possível para eliminar a linha ou coluna que esgotar a fonte ou preencher o requisito. Se ambos os satisfazem, elimine qualquer um deles. Se a menor célula de custo não for única, selecione arbitrariamente qualquer célula com menor custo.
Passo 2:
Repita o procedimento para todas as linhas e colunas não cruzadas com a próxima célula de menor custo. Etapa 3: Repita o procedimento até que todas as fontes estejam esgotadas ou a demanda de todos os destinos esteja cheia.
Exemplo 4:
Resolva o seguinte problema pelo método de menor custo:

Método de Aproximação Vogel:
Este método é um método de penalidade ou remorso e é preferível, em relação aos outros dois métodos, que a solução básica inicial viável seja ótima ou muito próxima da solução ótima, portanto, o tempo necessário para calcular a solução ótima é reduzido.
Nesse método, a base de alocação é a penalidade de custo unitário, isto é, aquela linha ou coluna que indica a maior penalidade de custo unitário / a diferença entre o menor e o próximo maior custo é selecionada primeiro para fins de alocação. Desta forma, as alocações subseqüentes nas outras células também são feitas tendo em vista a maior penalidade de custo unitário.
A alocação é feita para minimizar o custo da penalidade. Várias etapas envolvidas são as seguintes:
Passo 1:
Calcular a penalidade para cada linha e coluna é feito simplesmente tomando a diferença entre o menor e o menor custo de transporte na mesma linha e coluna, ou seja, a diferença indica a penalidade a ser paga se a alocação não for feita para o custo mínimo critério.
Passo 2:
Selecione uma linha ou coluna com a maior penalidade e aloque o máximo possível para a célula de menor custo. Em caso de empate, uma célula de alocação máxima possível é escolhida primeiro
Etapa 3:
Risque a linha ou coluna depois de atender a demanda ou esgotar o suprimento a linha ou coluna restante é atribuída a um suprimento ou demanda zero. Qualquer linha ou coluna com suprimento ou demanda nula não pode ser usada para cálculos adicionais.
Etapas 4:
Repita as etapas 1 e 3 até que todas as fontes estejam esgotadas ou que todos os requisitos sejam atendidos.
Exemplo 5:
Uma manufatura quer enviar 8 cargas de seu produto dos centros de produção X, Y e Z para os centros de distribuição A, B e C, a milhagem da origem 0 até o destino D é a seguinte matriz.


Exemplo 6:
Encontre a solução ideal do seguinte problema de transporte obtendo a solução inicial com o método de aproximação de vogets:

Solução:
Vamos aplicar o método de aproximação de vogel. Problemas balanceados como oferta = Demanda = 50 unidades. Vamos aplicar o método de vogel como dado na tabela abaixo.

Custo de transporte = 2 x 15 + 9 x 15 + 20 x 10 + 4 x 5 + 18 x 5 x 475 unidades.
Verifique otimamente:
O teste de otimalidade pode ser realizado se duas condições forem satisfeitas,
1. Há m + n - 1 alocação, cujo m é o número de linhas, n é o número de colunas. Aqui m + n - = 6. Mas o número de alocação é cinco.
2. Essas alocações m + n-1 devem estar em posições independentes, ou seja, não deve ser possível aumentar ou diminuir qualquer alocação sem alterar a posição das alocações ou violar as restrições de linha ou coluna.
Uma regra simples para alocações em posições independentes é que é impossível viajar de qualquer alocação, de volta para si uma série de passos horizontais e verticais de uma célula ocupada para outra, sem uma reversão direta da rota. Pode ver-se que, no presente exemplo, a atribuição está em posições independentes, uma vez que não pode ser formado um ciclo fechado nas células alocadas.
Portanto, a primeira condição não é satisfeita e, portanto, a fim de satisfazer a primeira condição, teremos que alocar uma pequena quantidade E nas células vazias com o menor custo de transporte. Pode ser visto que t pode ser alocado na célula (2, 2) com custo de 7 unidades e ainda assim as alocações permanecerão na posição independente conforme descrito abaixo na Tabela 2.

Agora o número de alocações é m + n - 6 = 6 e elas estão em posições independentes. Anote a matriz de custo nas células alocadas. (Tabela 3)
Matriz de custo inicial para células alocadas. Escreva também os valores de u i e v j .

Pode ser visto na Tabela 5 que a avaliação celular na célula (1, 4) é negativa, isto é, -4, portanto, alocando ao custo de transporte da célula (1, 4), ser ainda mais reduzida.
Vamos anotar as alocações originais e a nova alocação proposta.

Pode ser visto na Tabela 6 que se alocarmos na célula (1, 4) um loop é formado como mostrado e alocamos 10 unidades para que a alocação na célula (2, 4) desapareça como mostrado abaixo na Tabela 7. Novo tabela de alocação se tornará

Custo de transporte = 5X 2 + 10X 1 1 + 10X 7 + 15X 9 + 5X 4 + 18 + 5 = 435 unidades.
Ou seja, o custo de transporte desceu de 475 unidades para 435 unidades.
Verifique otimamente:
Vamos ver se esta solução é ótima ou não? Para isso, duas condições devem ser verificadas
Nº de alocação = m + n- 1 = 6 (satisfeito)
Alocação na posição independente (satisfeita, uma vez que o circuito fechado para as células alocadas não é formado) Escreva o custo nos alocados todos e valores de ui e v j .

Pesquisa de Operação: Ferramenta nº 3. Problema de Atribuição:
Problema de atribuição é um tipo especial de problema de programação linear que lida com a alocação dos vários recursos para as várias atividades numa base de um para um.
Ele o faz de tal forma que o custo ou o tempo envolvido no processo é mínimo e o lucro ou a venda é o máximo. Embora o problema possa ser resolvido pelo método simplex ou pelo método de transporte, o modelo de atribuição oferece uma abordagem mais simples para esses problemas.
Em uma fábrica, um supervisor pode ter seis funcionários disponíveis e seis empregos para serem acionados. Ele terá que decidir qual trabalho deve ser dado a qual trabalhador. Problema forma uma a uma base. Este é um problema de atribuição.
Modelo de Atribuição:
Suponha que haja n facilita e n empregos. É claro que, neste caso, haverá n atribuições. Cada instalação ou trabalhador diz pode executar cada trabalho, um de cada vez. Mas deve haver determinado procedimento pelo qual a atribuição deve ser feita para que o lucro seja maximizado ou o custo ou os tempos sejam minimizados.

Na tabela, Co ij é definido como o custo quando o trabalho é atribuído ao trabalhador. Pode-se notar aqui que este é um caso especial de problema de transporte quando o número de linhas é igual ao número de colunas.
Formulação Matemática:
Qualquer solução viável básica de um problema de atribuição consiste em variáveis (2n - 1) das quais as variáveis (n - 1) são zero; n é o número de empregos ou número de instalações.
Devido a esta alta degenerescência, se resolvermos o problema pelo método de transporte habitual, será um trabalho complexo e demorado. Assim, uma técnica separada é derivada para isso. Antes de ir para o método absoluto, é muito importante formular o problema.
Suponha que X ij seja uma variável definida como

Método para resolver o problema (técnica húngara):
Considere a função objetiva do tipo de minimização.
As etapas a seguir estão envolvidas na solução desse problema de atribuição:
1. Localize o menor elemento de custo em cada linha da tabela de custos fornecida, começando pela primeira linha. Agora, esse menor elemento é subtraído de cada elemento dessa linha. Então, estaremos recebendo pelo menos um zero em cada linha desta nova tabela.
2. Tendo construído a mesa (como na etapa 1), pega as colunas da tabela. Começando da primeira coluna, localize o menor elemento de custo em cada coluna. Agora subtraia esse menor elemento de cada elemento dessa coluna. Tendo realizado o passo 1 e o passo 2, estaremos recebendo pelo menos um zero em cada coluna na tabela de custo reduzido.
3. Agora, as atribuições são feitas para a tabela reduzida da seguinte maneira:
(i) As linhas são examinadas sucessivamente, até que a linha com exatamente um (um) zero seja encontrada. A atribuição é feita para este único zero colocando o quadrado □ ao redor dele e, na coluna correspondente, todos os outros zeros são riscados (x), porque eles não serão usados para fazer nenhuma outra atribuição nesta coluna. A etapa é conduzida para cada linha.
(ii) Etapa 3 (i) agora executada nas colunas da seguinte forma: As colunas são examinadas sucessivamente até que uma coluna com exatamente um zero seja encontrada. Agora, a atribuição é feita para este único zero colocando o quadrado em torno dele e, ao mesmo tempo, todos os outros zeros nas linhas correspondentes são riscados (x) o passo é conduzido para cada coluna.
(iii) Os passos 3 (i) e 3 (ii) são repetidos até que todos os zeros sejam marcados ou riscados. Agora, se o número de zeros marcados ou as atribuições feitas forem iguais ao número de linhas ou colunas, a solução ideal foi alcançada. Haverá exatamente uma única atribuição em cada coluna ou sem qualquer atribuição. Neste caso, iremos para o passo 4.
4. Nesta fase, desenhe o número mínimo de linhas (horizontal e vertical) necessárias para cobrir todos os zeros na matriz obtida no passo 3.
O seguinte procedimento é adotado:
(i) Marque (V) todas as linhas que não possuam nenhuma atribuição.
(ii) Agora assinale (V) todas essas colunas que possuem zero nas linhas marcadas.
(iii) Agora, o tick marca todas as linhas que ainda não estão marcadas e que têm atribuição nas colunas marcadas.
(iv) Todos os passos, isto é, 4 (1), 4 (2), 4 (3) são repetidos até que não seja possível marcar mais linhas ou colunas,
(v) Agora desenhe linhas retas que passem por todas as linhas desmarcadas e colunas marcadas. Também pode ser notado que em uma matriz nxn, sempre menos de 'n' linhas cobrirão todos os zeros se não houver nenhuma solução entre eles.
5. No passo 4, se o número de linhas desenhadas for igual a n ou o número de linhas, então é a solução ideal se não, então vá para o passo 6.
6. Selecione o menor elemento entre todos os elementos descobertos. Agora, esse elemento é subtraído de todos os elementos descobertos e adicionado ao elemento que fica na interseção de duas linhas. Esta é a matriz para novas atribuições.
7. Repita o procedimento a partir do passo (3) até que o número de atribuições seja igual ao número de linhas ou número de colunas.